Les moteurs de recommandations font aujourd’hui partie de notre quotidien, qu’il s’agisse de Google, Amazon ou bien des commerçants en ligne, tous utilisent de près ou de loin des moteurs de recommandations. Les réseaux sociaux utilisent un moteur de recommandation pour vous proposer de nouvelles personnes à suivre, les sites de presse vous proposent des articles susceptibles de vous intéresser. Tout cela est basé sur des algorithmes mathématiques utilisant les données du site, l’article sur les recommandations permet de comprendre les objectifs et algorithmes utilisés par ces moteurs de recommandations.

Les différentes missions menées au sein de Kernix ont permis d’imaginer et de mettre en place différentes solutions en fonction des besoins clients et des différents types de variables. Devant la diversité des données présentes sur un site internet il n’est pas toujours évident de mettre en place un moteur de recommandation pertinent. Les textes et images doivent être transformés en vecteurs de grandes dimensions alors que des variables comme le prix ou la localisation géographique peuvent être représentés sur quelques dimensions. Les recommandations et leurs qualités dépendent principalement de la façon dont les variables sont transformées.

Une problématique cruciale est donc la gestion de la multimodalité : comment obtenir un moteur de recommandations performant lorsque les types de variables sont différents?
Nous allons donc voir une partie des méthodes utilisées par Kernix pour gérer la multimodalité : la réduction de dimensions, trois types de pondérations (des variables, des distances et du vecteur cible) puis nous finirons par évoquer les filtres.

Réduction de dimensions

Dans la littérature, les approches les plus utilisées sont les méthodes de réduction de dimension. La réduction de dimension permet, en utilisant les corrélations entre les différentes variables, de résumer les informations les plus importantes d’un vecteur en un nombre plus restreint de dimensions. Réduire le nombre de dimensions permet d’augmenter la rapidité du moteur de recommandations et de réduire le poids des données à stocker.

Les trois types de réduction de dimension principales sont :

• l’Analyse en Composantes Principales (ACP),
• l’Analyse des Correspondances Multiples (ACM)
• et l’Analyse Factorielle des Données Mixtes (AFDM).

L’ACP est utilisée lorsque les variables sont quantitatives, alors que l’ACM est utilisée lorsque les variables sont qualitatives. La méthode FAMD est une méthode combinant l’ACP et l’ACM pour s’adapter aux données mixtes (quantitatives et qualitatives).

Ces méthodes sont basées sur l’étude des corrélations entre les variables et donc s’adaptent difficilement lorsque les variables possèdent un déséquilibre de dimensions. Le moteur de recommandation sera pertinent si les catégories de variables possèdent à peu près le même nombre de variables (3 variables pour la géolocalisation: latitude, longitude et altitude, 2 variables pour la taille: longueur et largeur, 3 variables pour la couleur: code RVB, etc…).

Si, maintenant, on se place dans un cas où les recommandations doivent être effectuées sur un texte et quelques variables numériques, alors les méthodes décrites précédemment ne pourront pas concilier les deux types de variables. En effet, un texte une fois transformé est codé sur plusieurs centaines de variables, ainsi son influence sera bien trop élevée par rapport aux autres variables.
C’est pour répondre à ce problème que l’Analyse Factorielle Multiple (AFM) a été développée. Cette méthode permet de combiner l’ACP et l’ACM en pondérant les variables de sorte que les contributions au premier axe des groupes de variables soient égales. Elle permet donc d’équilibrer l’influence des différents types de variables.

Pondération des variables

Une autre solution, qui peut permettre de régler le problème de déséquilibre, consiste à pondérer les variables, c’est-à-dire à multiplier par un scalaire chaque valeur prise par la variable. Cela peut permettre à l’utilisateur de faire varier les résultats en fonction de ses envies. Il est important de noter que le choix des pondérations est crucial et qu’en fonction du nombre de variables et de leurs échelles, il peut être nécessaire de faire varier les pondérations avec une grande amplitude.

Cette méthode est très efficace et permet d’obtenir des résultats très divers et potentiellement adaptés à toutes recherches. Cependant à chaque changement de pondération le moteur de recommandations doit être ré-entraîné. Ainsi, cette méthode pourra être difficilement envisageable lorsque l’on recherche de la rapidité et qu’un passage à l’échelle est envisagé.

Distances pondérées (dite de Gower)

Une autre solution pour combiner plusieurs types de variables est d’utiliser différentes distances pour chaque type de variable. En effet, il existe plusieurs types de distances et en fonction des types de variables et des besoins. Il est important d’adapter la distance. Pour comparer deux textes codés sur trois cents dimensions, on privilégiera, par exemple, la distance cosinus alors que pour mesurer la distance entre deux prix, on adoptera plutôt la distance L1 (aussi appelée distance de Manhattan).

Les distances usuelles utilisées en fonction du type de variable sont résumées dans ce tableau :

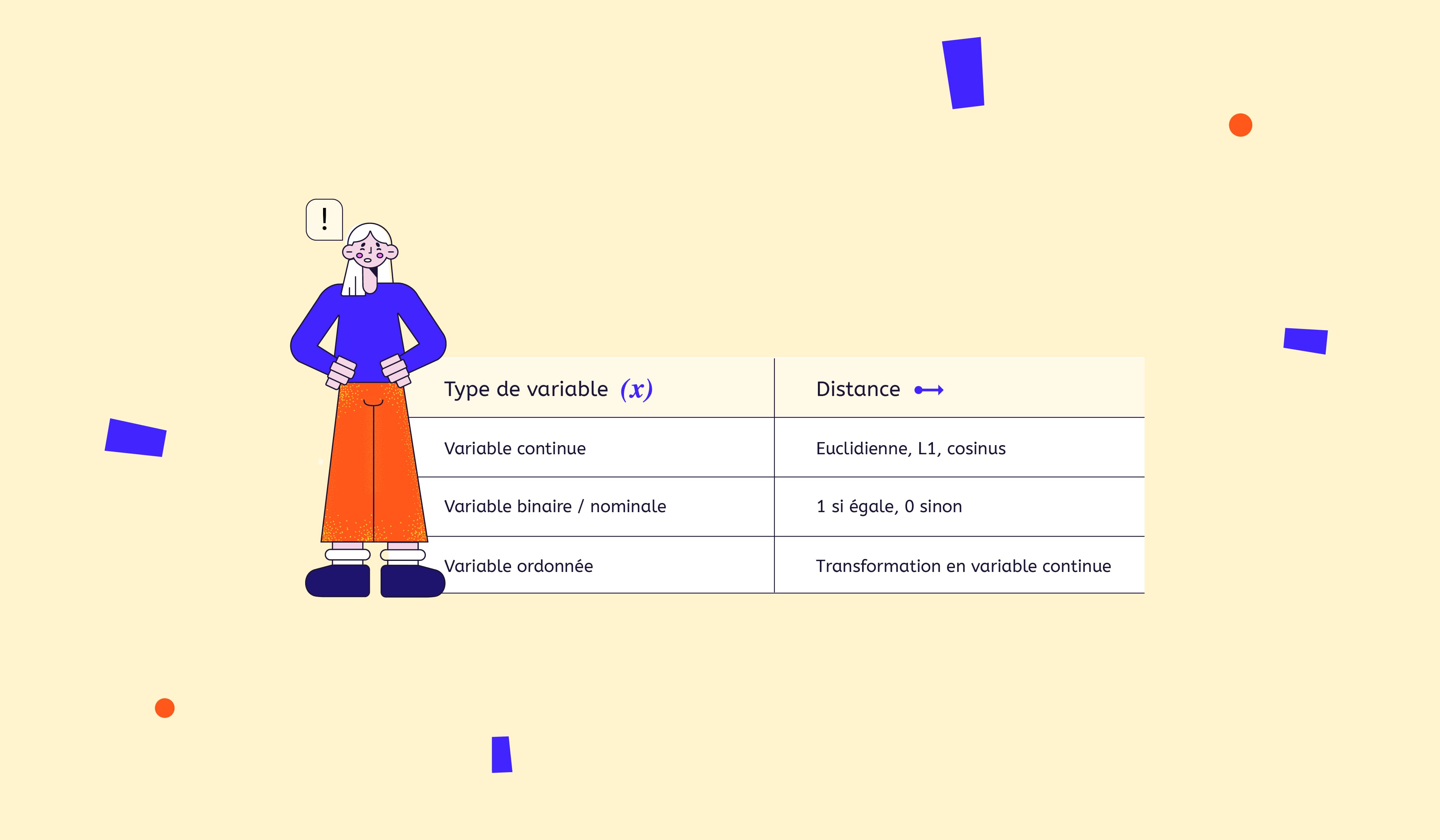
Ainsi, pour chaque type de variable, il sera possible de calculer une distance différente, une fois ces distances calculées on pourra alors les combiner en les pondérant pour obtenir une unique mesure de distance. Il existe plusieurs façons de combiner les différentes distances, une des plus utilisées est la distance de Gower.

La distance de Gower combine différentes distances en les pondérant non seulement par un poids mais aussi par l’inverse du nombre de variables ayant le même type. Il reste donc à choisir les distances à utiliser pour chaque type de variable ainsi que les pondérations :

Dans cette formule:

• p représente le nombre de types de variable.
• wi est le poids associé aux variables de type i.
• ni est le nombre de variables de type i.
• di est la distance associée aux variables de type i.
• Xi et Yi sont les sous-vecteurs de X et Y associés aux variables de type i.

Une fois de plus, cette méthode permet d’avoir un panel de recommandations très large. Cependant, les inconvénients présentés dans la partie précédente sont toujours présents : le modèle doit être ré-entraîné à chaque changement de pondération dont le choix ne s’avère pas toujours évident.

Notre astuce : pondération du vecteur cible

Afin de laisser un maximum de libertés à l’utilisateur, il est possible de transformer la méthode précédente afin que les pondérations soient déterminées par l’utilisateur sans perte d’efficacité. L’article de (Wang et al. 2021) présente une méthode permettant de pondérer les distances en ne changeant que les valeurs du vecteur cible. Ainsi, la base de données n’est jamais modifiée et l’utilisation est donc relativement simple.

La théorie derrière cette méthode est assez simple. Une fois les distances choisies, il faut transformer la formulation pour l’exprimer sous forme d’un produit scalaire.
Ensuite, en utilisant la bilinéarité du produit scalaire, on ne fait apparaître les pondérations que dans le vecteur cible. Afin d’utiliser cette méthode, il faut parfois adapter les distances.
Dans l’exemple qui suit, devant l’impossibilité d’utiliser la distance euclidienne, nous avons utilisé la distance euclidienne au carré. La preuve que la distance euclidienne au carré et la distance cosinus peuvent être transformées en produit scalaire est la suivante (on considère ici que les vecteurs U’ et V’ sont unitaires) :

Ici, le vecteur U représente le vecteur cible et le vecteur V, les vecteurs de la base. U’ et V’ représentent les composantes du premier type de variable (textuelles par exemple). U” et V” représentent les composantes du second type de variable (géographiques par exemple). 𝛼 représente la pondération associée au premier groupe de variable et 𝛽 représente la pondération associée au second.

Cette transformation permet d’utiliser pour le moteur de recommandation une unique mesure de distance, le produit scalaire, équivalent à la somme pondérée de plusieurs distances.
À noter que la base de données doit être modifiée afin que le produit scalaire soit équivalent à la pondération des distances.

Dans l’exemple précédent, il faut ajouter trois colonnes à la base de données, deux colonnes contenant uniquement la valeur 1 et une colonne correspondant au carré de la norme 2 du sous-vecteur V”. Une fois cette transformation effectuée, l’utilisateur peut choisir ses pondérations et adapter ses recherches en fonction des résultats obtenus. Cette méthode présente cependant deux complications : la première étant que l’on ne peut pas utiliser toutes les distances. La deuxième repose sur la difficulté que peut rencontrer l’utilisateur à trouver de bonnes pondérations pour obtenir des recommandations pertinentes.

Filtres

La dernière méthode présentée ici est peut-être la plus simple mais est néanmoins souvent assez efficace. Afin de s’assurer de la pertinence des résultats, il est possible de mettre en place des filtres afin de présélectionner des données.

Les filtres peuvent être effectués de différentes manières, la plus simple est de sélectionner un sous-ensemble de lignes correspondant aux plages de valeurs souhaitées. Ainsi, le moteur de recommandation sera appliqué à un ensemble d’individus respectant un critère de sélection, ce qui assurera le fait que les résultats soient cohérents avec la demande. Cette méthode est assez efficace, cependant elle peut poser quelques problèmes. D’une part, si c’est l’utilisateur qui choisit les sous-ensembles de valeurs alors le travail peut devenir long et fastidieux. Il faut tout d’abord sélectionner les variables à discriminer, puis, pour chaque variable, lui associer une plage de valeurs. D’autre part, si les sous-ensembles sont prédéfinis, alors l’utilisateur n’a plus vraiment de libertés pour adapter les résultats en fonction de ses envies.

Une deuxième façon de gérer la multimodalité par filtre est d’effectuer une première recommandation en utilisant une partie des variables seulement, puis d’ordonner les résultats selon les autres variables. Cette méthode peut s’avérer très utile lorsque le nombre de variables est très important. En effet, plutôt que d’utiliser la première méthode et de devoir définir une plage de valeurs pour un grand nombre de variables, le sous-ensemble est calculé de manière automatique. De plus, la méthode peut être adaptée en fonction des envies car les variables utilisées pour créer le sous-ensemble ou pour ordonner les résultats peuvent varier, tout comme la taille du sous-ensemble.

Les filtres sont donc très utiles pour réduire rapidement l’horizon des recherches ou bien lorsque le nombre de variables est assez important. De plus, les filtres s’adaptent très bien au passage à l’échelle car ils restent efficaces lorsque le volume des données augmente. Il faut cependant garder en tête que les filtres hiérarchisent certaines variables. Les variables permettant d’ordonner le sous-ensemble final auront un impact plus important que les autres.

Conclusion

La création de moteurs de recommandation lorsque les données sont multidimensionnelles peut s’avérer complexe. Vous l’aurez compris, les choix à faire dépendent du type de données mais aussi des souhaits du ou des utilisateurs. Les méthodes de réduction de dimension sont efficaces lorsque les nombres de dimensions des différentes données sont relativement équilibrés. Si l’on doit gérer des textes transformés en plusieurs centaines de variables, alors les méthodes les plus appropriées sont les filtres ou les pondérations, notamment du vecteur cible.

Lorsque l’utilisateur a des envies précises et arrêtées sur certaines valeurs de variable, alors les filtres sont la meilleure solution. Dans le cas contraire, lorsque l’utilisateur souhaite pouvoir modifier les recommandations en fonction de ses envies, la mise en place de moteurs de recommandation basé sur la pondération du vecteur cible est intéressante.

C’est dans cette idée qu’au sein de Kernix ces études ont été menées et testées afin de toujours essayer de trouver la solution qui convient le mieux aux besoins de l’utilisateur en fonction des données disponibles.