Le graphe :

Le graphe est avant tout un object mathématique aux nombreuses applications, ainsi qu’une structure de données bien connue en informatique.

On le retrouve partout, comme le confirment ces quelques exemples :

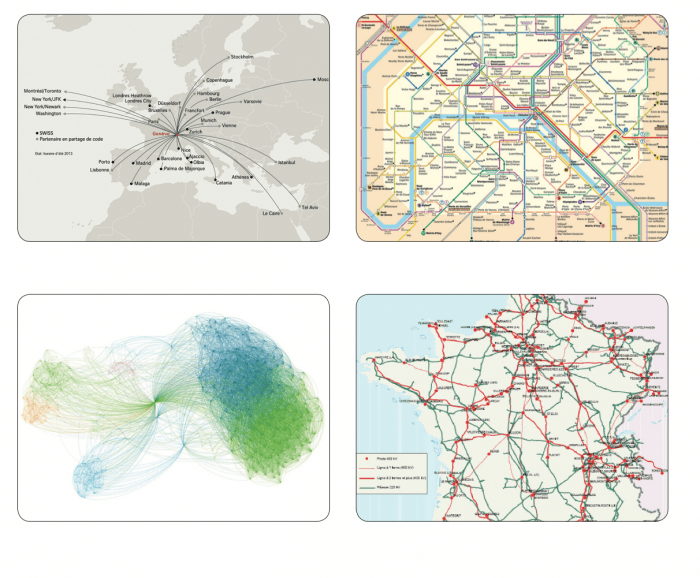
Au-delà de sa valeur illustrative, il s’agit d’un outil extrêmement puissant pour extraire de l’information et en tirer de la connaissance, tout en restant assez intuitif et accessible (ce que toute personne qui s’est amusée un jour à expliquer quelque chose en dessinant des ronds et en les reliant avec des flèches a pu constater !).

La définition est très simple : il s’agit simplement d’un groupe de noeuds/sommets reliés entre eux par des arcs/arêtes, qui peuvent être ou non orientés. Le réseau social d’un individu sur facebook est un graphe non-orienté, la relation d’amitié étant symétrique, tandis que sur twitter, il s’agit d’un graphe orienté, puisqu’on peut suivre quelqu’un sans que celui-ci nous suive en retour.

Extraire l’information des données connectées :

Maintenant que nous avons posé le contexte, et défini les graphes de façon plus concrète, examinons les informations que nous pouvons en tirer.

Chemins et distances :

La première application à laquelle on pense souvent est la recherche de chemin entre 2 noeuds, à l’image de ce que font les GPS pour calculer des itinéraires. Mais on peut également chercher le degré de séparation entre 2 personnes, faire de la planification et de l’optimisation, ou de l’arbitrage financier.

La notion de distance est centrale pour plusieurs types d’analyses de données, et il n’est pas toujours évident de la définir pour des données hétérogènes et non-structurées. La distance entre deux éléments est au contraire assez naturelle à définir au sein du graphe.

Centralité des noeuds :

L’étude de la “centralité” des noeuds au sein d’un réseau trouve son origine dans l’analyse de réseaux sociaux, lorsque des chercheurs s’essayaient, à partir des relations entre individus, à identifier les personnes influentes. Le graphe n’étant pas défini à travers un système de coordonnées extrinsèque, la hiérarchisation des noeuds doit nécessairement se faire à partir des informations intrinsèques, comme la situation des noeuds les uns vis-a-vis des autres.

Cette notion de centralité trouve des applications très variées, que cela soit dans l’algorithme pagerank de google, qui définit l’autorité d’une page web à travers les liens qui pointent vers elle, dans l’identification de noeuds sensibles au sein d’un réseau telecom ou dans les réseaux de transport, mais aussi pour comprendre la propagation de virus ou d’informations dans des réseaux humains.

Analyse structurelle :

La structure du réseau au voisinage d’un noeud est un marqueur de la nature de ce noeud. Les relations témoignent de son rôle à travers ses “activités” et ses “interactions” avec le reste du réseau.

C’est cette propriété qui fait la puissance du graphe dans l’analyse de données complexes, et qui expliquent son adoption dans des domaines pointus comme la biologie, pour comprendre les interactions entre les gènes, ou dans les métiers bancaires, pour la détection de fraude.

Elle permet également d’identifier des relations absentes du graphe, mais qui sont fortement probables, comme ce qu’on retrouve sur les sites de réseaux sociaux lorsqu’ils nous suggèrent de nouveaux amis potentiels.

Clustering :

Le clustering sur le graphe a un intérêt particulier, parce qu’il se base sur les propriétés structurelles dont nous avons parlé au paragraphe précédent. Nous avons signalé plus haut que la notion de distance était naturelle sur un graphe, en considérant le voisinage d’un nœud.

Il est plus facile d’identifier les éléments avec le plus d’affinité, ou des communautés à travers leurs interconnexions.

Ces analyses de graphe peuvent paraître bien abstraites au premier abord, et nous aurons l’occasion d’explorer plus en détail les nombreux outils que nous offre la technologie du graphe, ainsi que quelques cas d’usages intéressants, qui permettront de se faire une idée de ce qu’il est possible ou non de faire, et mieux comprendre les nouvelles perspectives qui s’ouvrent à nous .