-
Guillaume Bruneval,
- Stanislas Morbieu,
Publié le 08/09/2021
Souvent sollicité pour des problématiques de recommandation, Kernix a acquis au fil des missions une connaissance solide du sujet et souhaite aujourd’hui en faire bénéficier ses lecteurs en publiant une série d’articles en lien avec cette thématique. Ce deuxième article traite de manière générale de l’algorithme des plus proches voisins (souvent appelé KNN pour k-nearest neighbors), de ses versions approchées (ou AKNN pour approximated k-nearest neighbors) qui vont souvent permettre le passage à l’échelle et du nouveau framework qui permet de les exécuter de manière simple, optimisée et ergonomique : Milvus.
La recherche de proches voisins est une des méthodes les plus utilisées pour opérer une recommandation. Elle a aussi le bon goût d’être l’une des plus simples. Exposons-en rapidement le principe général. Imaginez que vous ayez lu un livre et que celui-ci vous ait beaucoup plu, à tel point que vous souhaitez en lire trois autres qui lui ressemblent le plus possible. Votre libraire virtuel, derrière lequel se cache une intelligence artificielle, va considérer un certain nombre d’informations sur les livres qu’il a en stock, il va les numériser de sorte que chaque livre soit représenté par un vecteur numérique. Il va ensuite calculer la distance entre le livre que vous avez aimé et tous les autres livres qu’il a en stock, avant de vous ramener les trois livres pour lesquels cette distance est la plus petite. On voit ici l’intérêt d’une telle méthode à des fins de recommandation. Ce n’est, du reste, pas son seul champ d’application, puisqu’il peut être utilisé pour effectuer des tâches de classification (détection d’anomalie, prédiction d’achats, articles scientifiques dignes d’intérêt pour un chercheur…). Son principal inconvénient demeure la lenteur puisqu’il effectue beaucoup de calculs qui, en définitive, ne lui serviront à rien. Ne pourrait-on pas, d’ailleurs, écarter un certain nombre de solutions qui de toutes évidences ne conviennent pas, sans avoir à calculer leurs distances à notre cible ? C’est ce que tentent de faire les méthodes de plus proches voisins approchées.
Pour mieux fixer les choses, tentons de les expliquer graphiquement, le processus est assez intuitif. Dans l’exemple ci-dessous, nos éléments sont représentés par des points dans un plan en deux dimensions. On a déterminé nos 20 plus proches voisins en comparant les distances avec celles de tous les autres points.
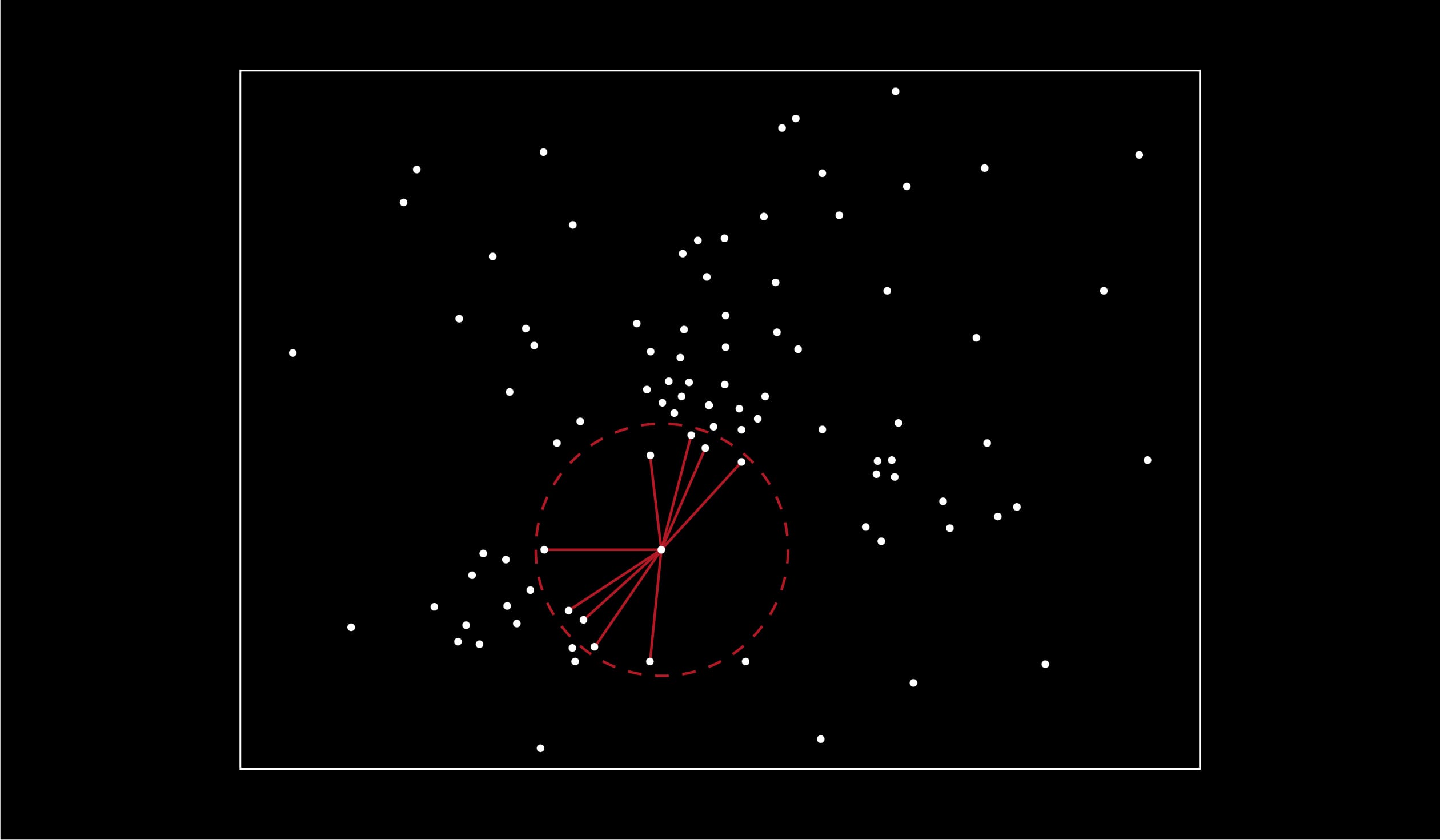
L’idée est très simple : au lieu de fouiller l’ensemble de l’espace des éléments candidats, nous n’en fouillons qu’une petite partie dans laquelle nous savons que l’élément cible se trouve. Cela implique que ces parties aient été déterminées au préalable, c’est-à-dire que notre espace ait été partitionné.
Le partitionnement consiste à morceler l’espace en de multiples sous-espaces. Reprenons notre graphique précédent et fragmentons l’espace :
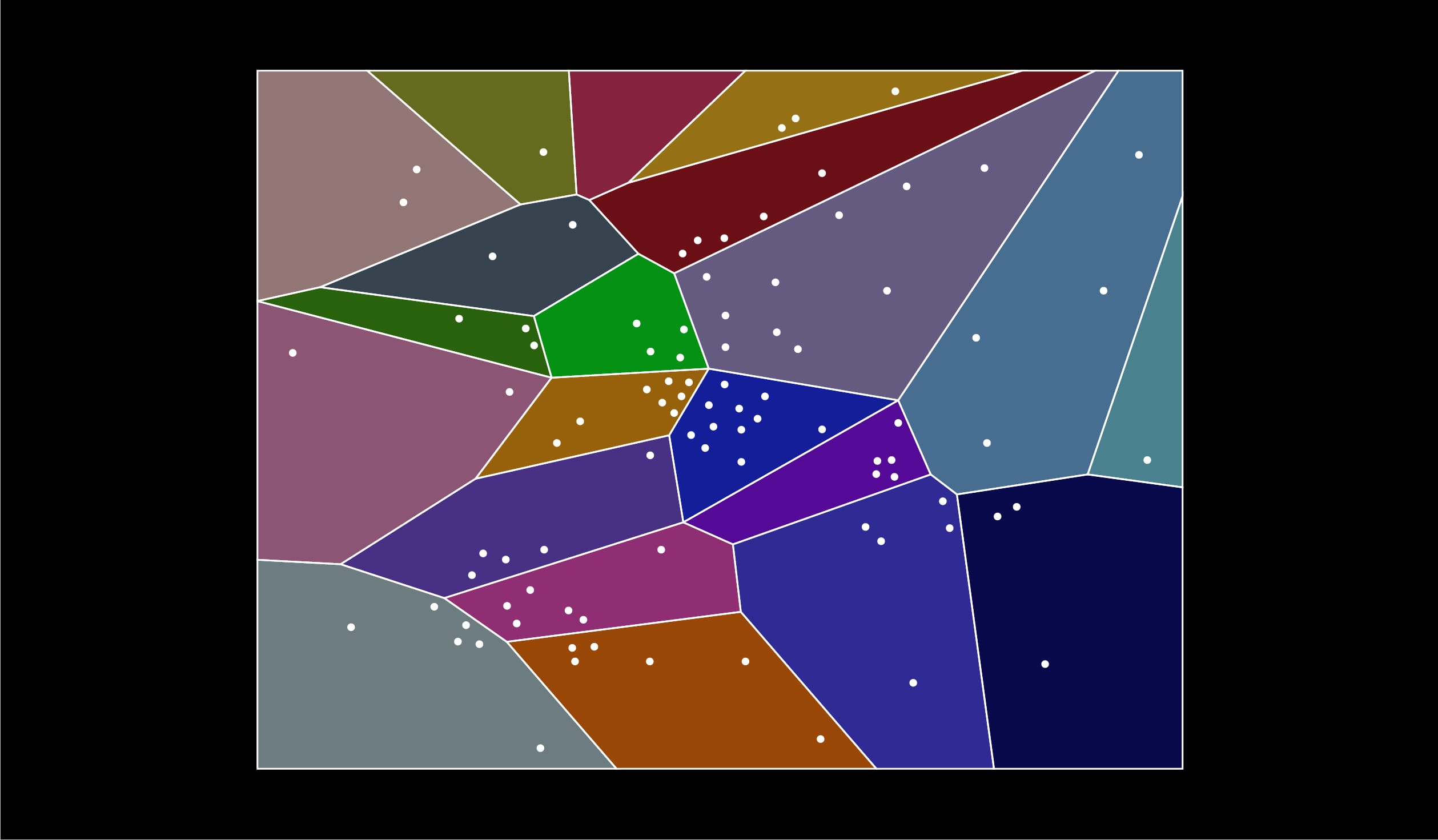
On recherche alors les plus proches voisins d’un élément uniquement dans un fragment ou que l’on appellera ici “cluster” :
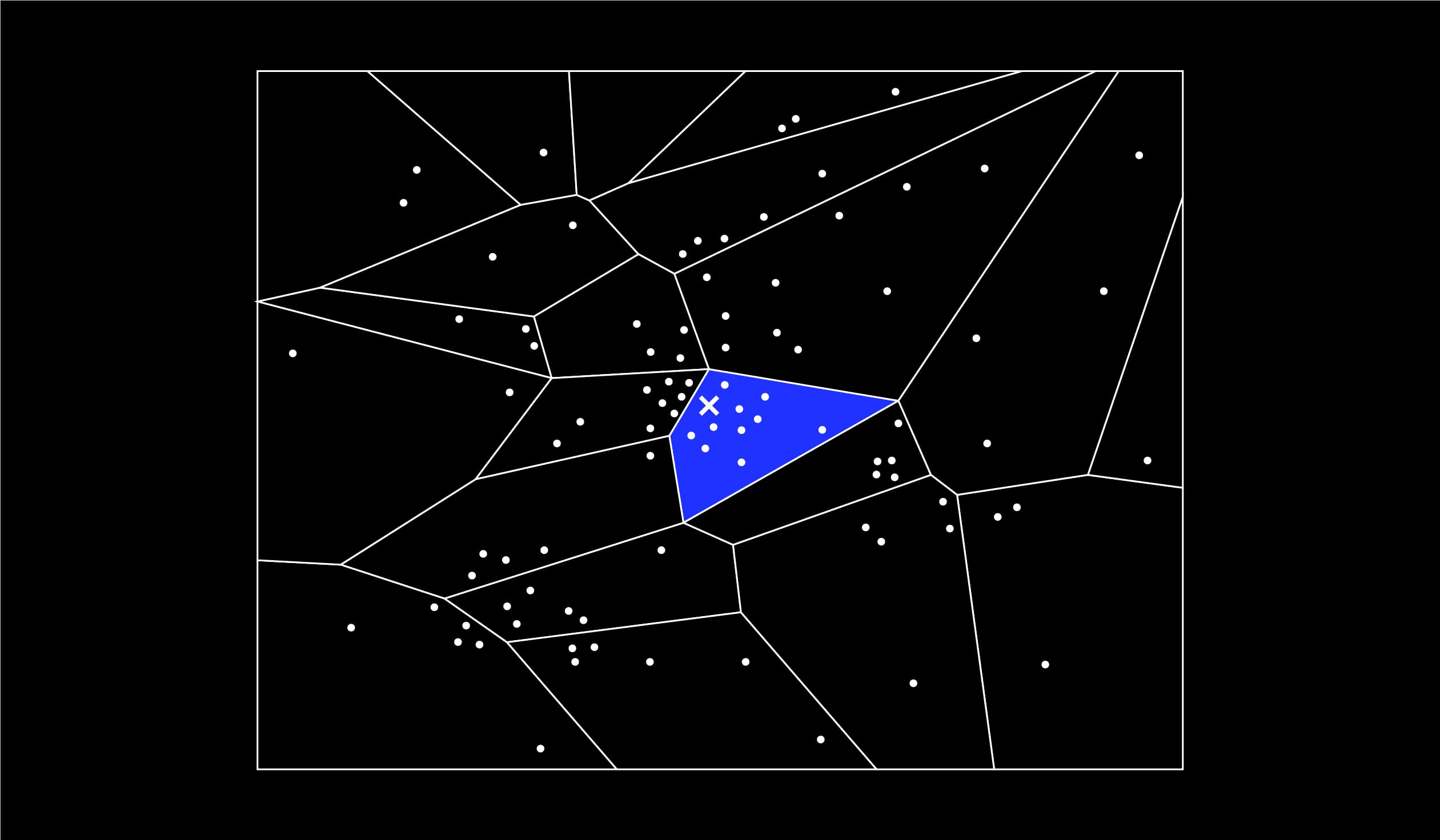
Mais que faire si le cluster dans lequel je vais fouiller ne compte que six éléments alors que je souhaiterais faire émerger les dix plus proches voisins ? Et que faire si l’élément cible se trouve, par un malheureux hasard, près de la frontière du cluster et que ses plus proches voisins se trouvent en réalité … de l’autre côté de cette frontière ?
C’est évidemment un écueil que l’algorithme anticipe et qu’il permet d’éviter. Comment ?
Là aussi c’est assez simple, en allant fouiller les clusters adjacents, c’est-à-dire les clusters qui ont une frontière commune avec le cluster cible. Si l’on juge que ces clusters sont trop nombreux, on ne peut fouiller que les clusters qui partagent la frontière commune la plus proche du point cible. Et en pratique on va les fouiller selon un ordre défini par une “file de priorité” définie par la distance du centre de gravité de chaque cluster au point cible. “Mais alors on recalcule des distances alors qu’on voulait justement en calculer moins !” nous objecterez-vous à juste titre. Oui, c’est vrai, mais il vaut mieux calculer les distances à quelques centres de gravité plutôt qu’à des millions de points.

On l’aura compris notre recherche est extrêmement dépendante de la manière dont on va partitionner l’espace. Alors pour se prémunir d’un partitionnement un peu fantaisiste, on va en combiner plusieurs. Les partitionnements pouvant, entre autres, être obtenus grâce à des arbres de décision (ce que nous aborderons ultérieurement), on appelle cela tout naturellement des forêts de partitionnements. On applique les principes de “clusters adjacents” et de “file de priorité“ pour chaque partitionnement, on opère une réunion des clusters obtenus et on obtient alors le polygone ci-dessous dans lequel on va appliquer l’algorithme des plus proches voisins.
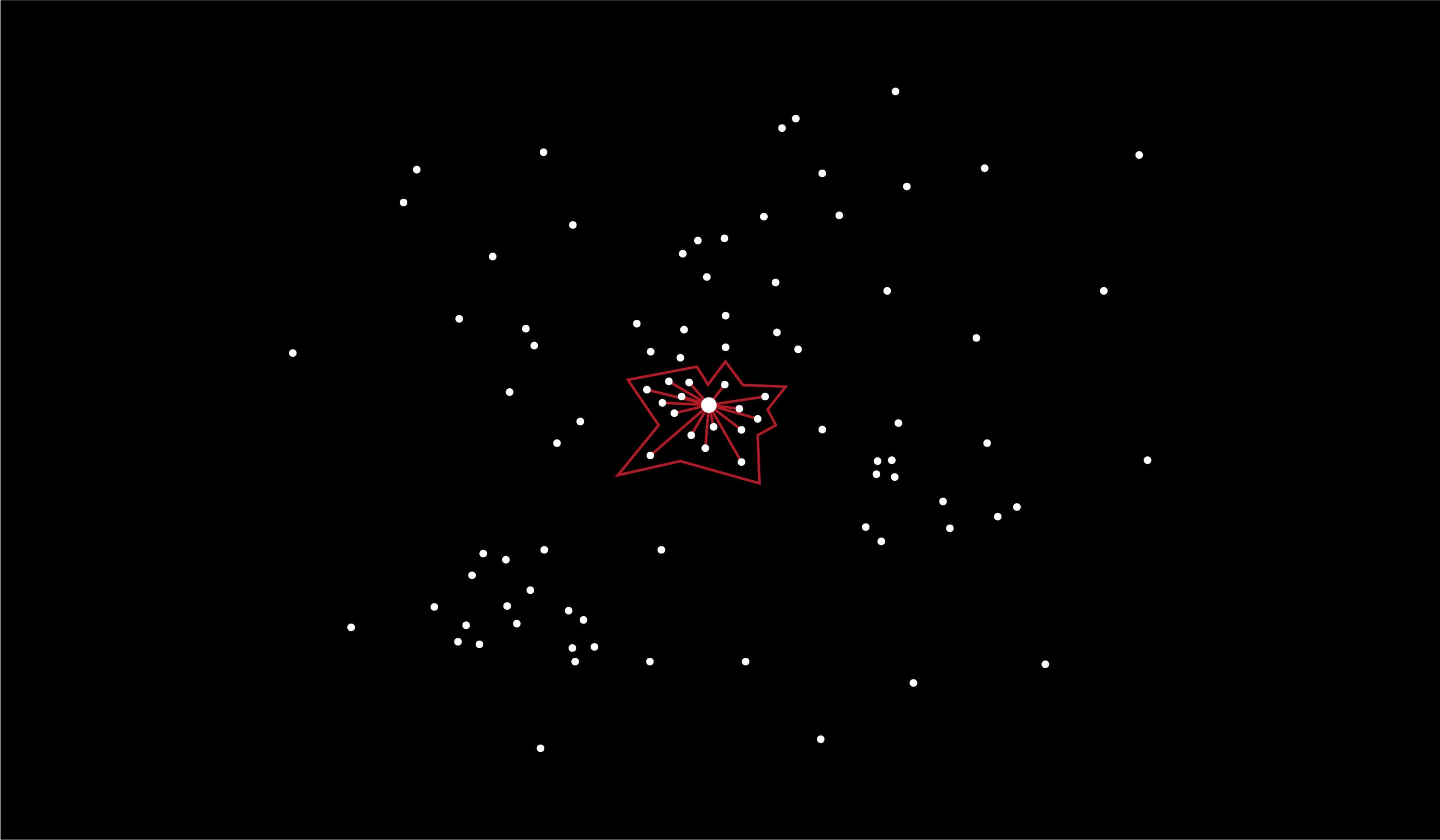
Et voici comment on peut diviser grandement son nombre de distances à calculer et donc son temps d’exécution. Dans le cadre de la construction du moteur de recommandation de sociétés que nous avons effectué, cela nous a permis de faire baisser notre temps de requête d’environ 800 à 100 millisecondes. Un gain précieux quand on sait qu’au-delà de 150 ms d’attente, on considère que l’utilisateur ressent une gêne et va statistiquement finir par ne tout simplement plus utiliser le système.
Simple n’est-ce pas ?
Simple oui, sur le plan théorique. Mais sur le plan pratique, c’est beaucoup plus complexe. Les deux grandes questions étant : comment et surtout quand effectuer les partitionnements ?
Il existe de nombreuses façons de partitionner l’espace, mais, sans rentrer dans les détails, disons qu’il existe quatre grandes familles d’approches :
“Seconde objection” seriez-vous en droit de nous dire, “n’est-il pas ubuesque, dans l’optique de simplifier nos calculs d’avoir recours à des méthodes complexes comme le clustering, le hashing ou la construction d’arbres aléatoires ?” Et bien nous répondrons cette fois que non, parce que ces tâches peuvent s’effectuer à d’autres moments que celui de la requête, quand le système est en repos, et donc ne pas impacter le confort de l’utilisateur. Par ailleurs, un seul entraînement va permettre d’effectuer autant de requêtes que l’on veut (jusqu’à ce qu’on décide de réentraîner parce que la base aura été mise à jour par exemple). Là, réside le secret et le succès des plus proches voisins approchés.
Il existe de nombreuses implémentations de l’algorithme des plus proches voisins approchés, l’une des plus célèbres versions, par exemple, est appelée Annoy et repose sur les arbres aléatoires. À Kernix nous sommes familiers depuis quelques années déjà de ces implémentations, mais l’année passée nous avons commencé à travailler avec un framework dont la version 2.0, en cours de finalisation fin 2021, nous est apparue comme particulièrement convaincante : il s’agit de Milvus.
Totalement open-source et doté d’une communauté dynamique, Milvus propose de nombreux avantages :
Auparavant, nous maintenions en interne à Kernix des solutions de recherche de plus proches voisins. Le projet open source Milvus nous permet de nous affranchir de développements conséquents autour des algorithmes : l’association entre les entités indexées par l’algorithme de plus proches voisins et celles stockées dans les autres bases de données, la gestion du déploiement sur plusieurs instances le cas échéant, la mise à jour des éléments supprimés à répercuter dans l’index, la fréquence d’entraînement du modèle, la conception d’une même API pour les différentes méthodes de recherche et d’indexation, etc. Les efforts sont désormais mutualisés dans un projet open source.
Les problématiques de recommandation sont indissociables de celles de passage à l’échelle. Les algorithmes des plus proches voisins approchés sont une des manières de répondre aux besoins de passage à l’échelle. Ils reposent sur des concepts simples, mais qui doivent être bien exécutés pour être efficaces. C’est la raison pour laquelle Kernix fait partie des “early adopters” de Milvus, et voit dans ce framework une solution agile, efficace et peu coûteuse dont nous espérons au plus vite faire bénéficier nos clients. Alors prêts à essayer Milvus ?